Training a neural network using tensorflow-privacy to predict diabetes outcomes

We train a neural network using the tensorflow-privacy library to predict diabetes outcomes while maintaining a good guarantee of privacy. We use the Pima Indians Diabetes Database to train models both with and without Differential Privacy. You can clone this google colab notebook to train the model yourself.

About the Pima Indians dataset

You can find the dataset in the Kaggle website. The data was collected by the National Institute of Diabetes and Digestive and Kidney Diseases. It was curated from a larger database and it contains only information on adult female patients of Pima Indian Heritage. The dataset has 8 input variables that are used to predict the outcome, wich is wheter or not a patient has diabetes.

Initial data analysis

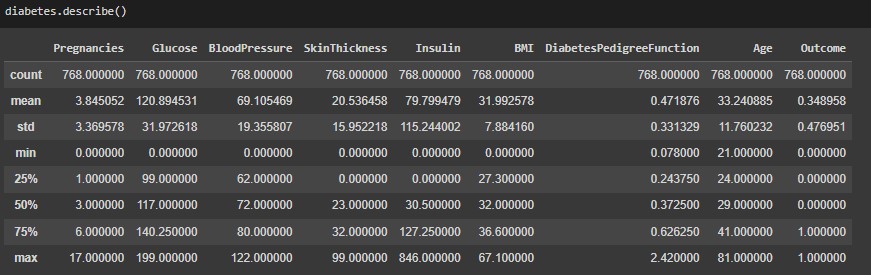We start by checking the first 5 rows in order to familiarize ourselves with the data:Checking the data using Pandas describe function:Checking for null values:

Data cleaning

In order to train the models and achieve better accuracies, we need to clean the data by either removing or transforming invalid values, checking for outliers and correlations.

Working with invalid zero values

Albeit there are no null values, we still have to check for invalid values, such as "0" for glucose, blood pressure, skin thickness, insulin and BMI.
We can achieve this by looking at the histograms:

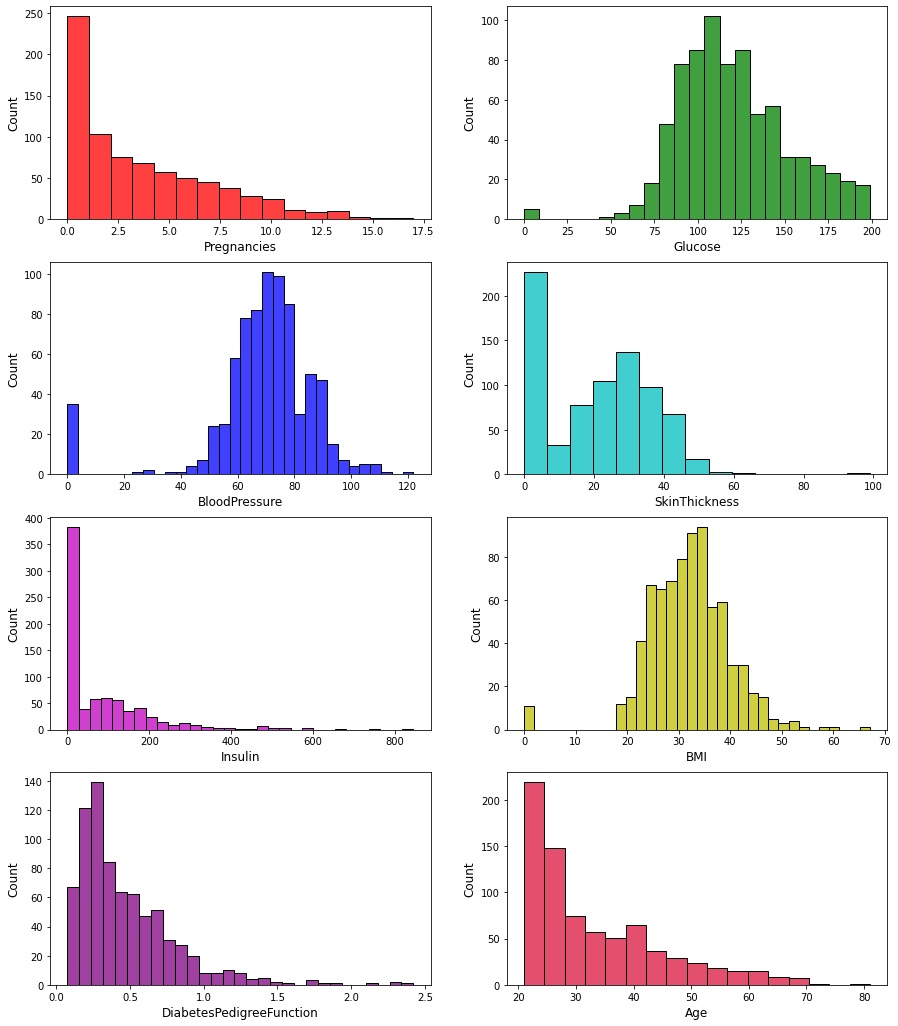We can see that there are several zero values for columns where there should not be any. In particular the insulin column has more than 350 zeros. These rows can't be regarded as invalid as the dataset is already small enough. Instead we are going to replace the zeros with the means of each corresponding columns: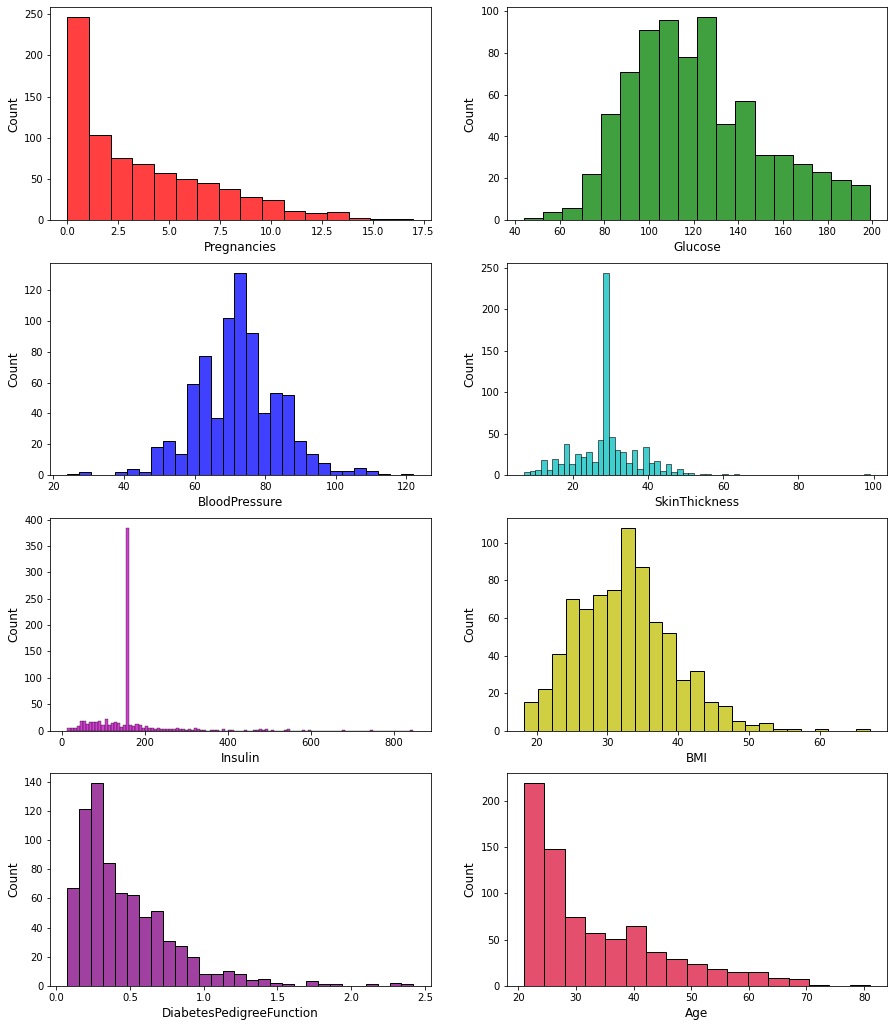

Checking for Outliers

In order to identify outliers we are going to use boxplots: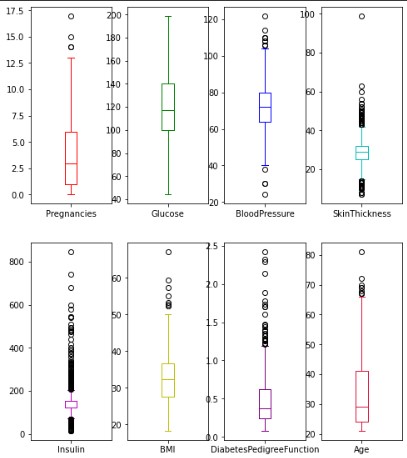

Then we remove the outliers that are under or over the 0.2 and 0.8 quantiles:

The result is that 105 rows were removed from the dataset, leaving it with 670 rows

Checking correlations

We can check for correlations between the input variables using a heatmap: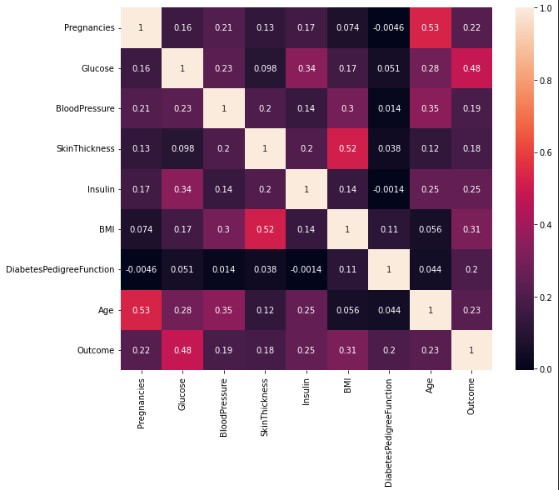

High correlations are seen between several columns belonging to the input group. For example: Skin width with BMI (0.52), Glucose with Insulin (0.34) and Age with Pregnancy (0.53). These correlations should be taken into account when regularizing the models, i.e. using a Ridge L2 regularizer.
We can list the correlations with the outcome variable:

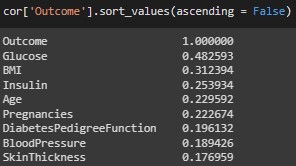Based on the guidelines of Schober et al in Correlation Coefficients: Appropriate Use and Interpretation (Schober et al., 2018); All correlations are in the medium to weak range, however, in context none can be said to be negligible, as none is less than 0.1 and the highest is only 0.48. Therefore, no columns are eliminated.

Normalizing the data

Neural networks are sensitive to the scale of the input data. Therefore, we need to normalize the data in order to achieve faster convergence and better results -in terms of privacy, we will see why later-. We can either use the MinMaxScaler from sklearn or do it ourselves by subtracting the mean and dividing by the standard deviation. We are going to use the latter: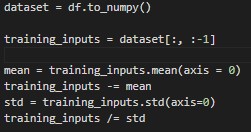

Training and validation split

Using the train_test_split function from sklearn, we split the data into training and validation sets: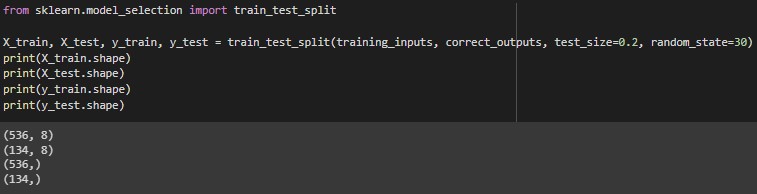

Training the model without using TensorFlow without Differential Privacy

With the dataset cleaned, normalized and split, we can now train the model. We are going to use the Keras Sequential API and TensorFlow to build the neural network. It will have an input layer with 8 neurons, 3 ReLu activation hidden layers (100, 25 and 10 neurons respectively) and an output layer of sigmoid activation with 1 neuron: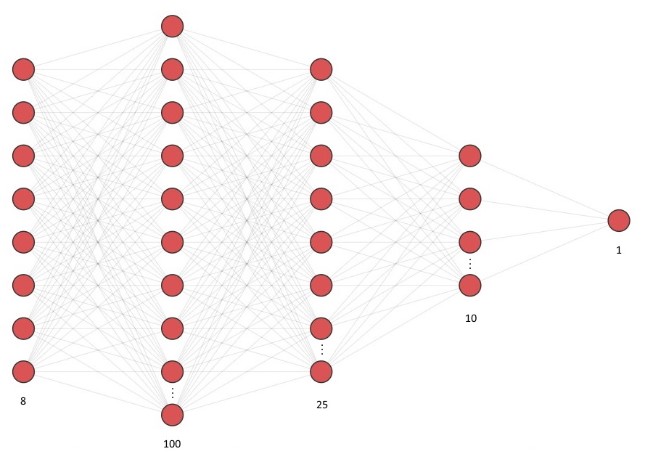At just 36 epochs a validation accuracy of 82.09% was achieved, and the model is well fit: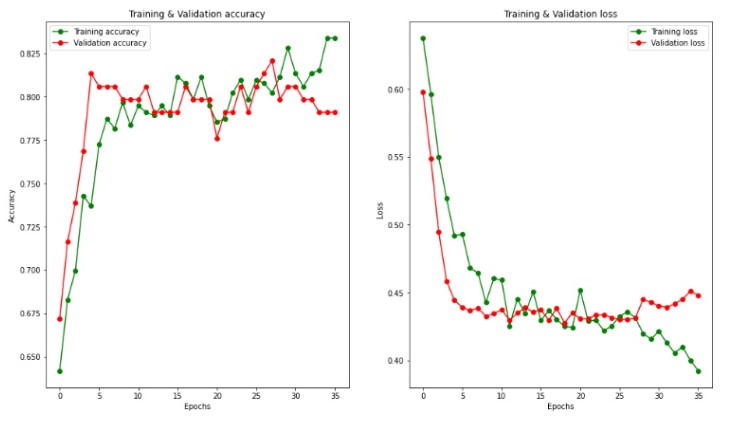

Training the model using TensorFlow with Differential Privacy

In order to train the model with differential privacy, we need to add noise to the gradients of the model. We are going to use the DPKerasSGDOptimizerfrom the tensorflow-privacy library. This optimizer adds noise to the gradients of the model, and it is based on the SGD optimizer.

We are going to use the same model as before, but we are going to use the DPSGD optimizer instead of the vanilla SGD optimizer, with the following hyperparameters: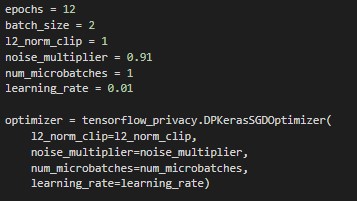

A validation accuracy of 80.59% was achieved, which is lower than the accuracy achieved without differential privacy. However, this model was trained with a mathematical guarantee of privacy (epsilon=7.31, delta=0.001), which is a good epsilon, but not quite perfect deniability (delta must be less than 1). The model is well fit: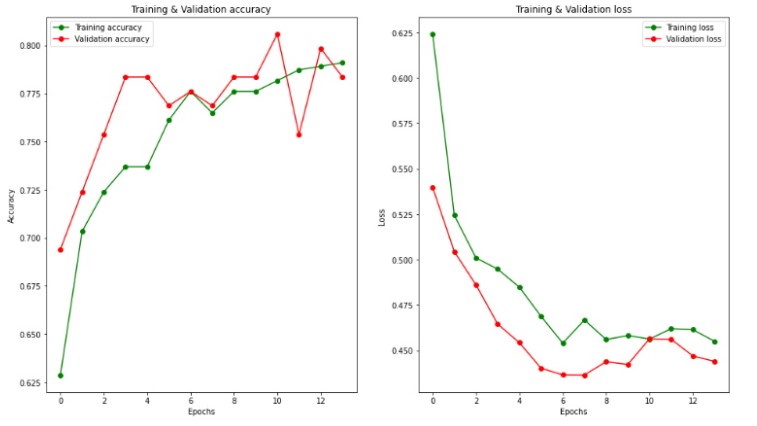Notice that the model converges in only 12 epochs, this was achieved by cleaning and normalizing the data, using a smaller learning rate and a smaller batch size.
The idea behind getting a smaller number of epochs is that epsilon (and therefore differential privacy guarantees) is inversely proportional to the number of epochs. Therefore, if we can get the same accuracy with less epochs, we can get a better epsilon.

Conclusions

In this article we have seen how to train a neural network with differential privacy using TensorFlow. We have seen how to clean and normalize the data, and how to train the model with and without differential privacy. We got a validation accuracy of 82.09% without differential privacy, and 80.59% with differential privacy. The model with differential privacy was trained with a mathematical guarantee of privacy (epsilon=7.31, delta=0.001), The tradeoff between accuracy and privacy is decent in this case, as only a 1.5% drop in accuracy was achieved, while getting a good epsilon (7.31).